什么是向量(Embedding)

向量是一个数据集合，用来表示一个事物的特征。比如，我们有一个班级的学生，每个学生有年龄、性别、身高、体重等特征，我们可以用一个向量来表示一个学生， 向量的每个维度对应一个特征，比如：[18, 1, 170, 60]，这个向量表示一个18岁、男性、身高170cm、体重60kg的学生。就这样我们可以把一些事物抽象出一些 特征属性来方便我们进行计算。比如我要找这个班级里面年龄最大的学生，那么我只需要找到年龄维度最大的向量就可以了。

我们可以把这种用向量表示一个事物的方法应用到更广泛的地方，比如图片，文本，音频等。比如我们有一张图片，我们可以用一个向量来表示这张图片，向量的每个维度 分别表示图片的一些特征，比如图片色阶直方图的分布，我们可以定量地表示这张图片的色彩分布，然后可以用这个向量来找到色彩相似的图片了。同样地，对于文本 数据，我们可以提取某个字出现的频次作为特征，这样就可以通过向量某个维度排序来找到某个字频次最高的一句话了。

当然，实际应用中我们不会这么简单地用一两个维度来来表示一个事物，我们会用更多的维度来表示，甚至使用了 "玄学" 来提取特征，如使用 CNN 的最后一层卷积层 作为特征向量。这些特征向量的提取方法不是本文的重点，不做展开。 这里推荐一个比较好玩的 CNN 可视化工具 CNN Explainer。

如何做向量检索

假设我们有一个向量集合，我们要找到与某个向量最相似的向量，这个问题就是向量检索。一般地我们都是找数据集中与用户请求 Query 中最相似的向量，这种问题叫 TopN 检索。而向量 TopN 检索问题里面，分为 KNN(K-Nearest Neighbor) 和 ANN(Approximate Nearest Neighbor) 两种检索方式，KNN 是精确 检索，ANN 是近似检索。KNN 的检索较准确，但是计算量大，面对如今海量的数据处理起来不太科学。ANN 是一种近似的计算，可能会忽略掉最优的结果，但是给出的 结果也不会太差，而且计算量较小，适合大规模数据的检索。

向量检索问题其实就是这样，假设我们现在有一个向量集合来表示一堆文本的特征，现在需要找到与用户输入的文本最相似的文本，这个问题就是向量检索。现在我们有 的向量是：

[100, 200, 100, 100]
[200, 300, 200, 500]
[300, 400, 300, 400]
[400, 500, 500, 600]
[500, 600, 600, 200]

这时候用户输入了一个文本，我们使用一样的特征算法得出这个文本的特征向量是 [300, 200, 100, 400]，我们需要找到这个向量和存量向量集合中距离最小的 向量。一般距离计算有余弦距离和欧氏距离两种。欧氏距离注重的是向量的绝对值，对于数值大小变化很敏感；而余弦距离注重的是向量的方向，对于数值相对大小比较 敏感。这里我们使用欧氏距离来算，因为比较简单，计算公式如下：

$ d = \sqrt{\sum\limits_{i=1}^{n} (x_{i} -y_{i})^{2} } $

对于两个四维的点 x、y，距离如下：

$ d(x, y) = \sqrt{(x_{1} - y_{1})^{2} + (x_{2} - y_{2})^{2} + (x_{3} - y_{3})^{2} + (x_{4} - y_{4})^{2}} $

背景知识

K-means 聚类

K-mains clustering 的目标是将 n 个观测值划分为 k 个簇，其中每个观测值属于具有最近均值（簇中心或簇质心）的簇，作为集群。说人话就是，把一堆向量 划分成 k 个簇，每个簇选择一个点作为簇新，每个簇内所有向量到簇心的距离之和最小。

图片来源

K-means 的算法步骤如下：

1. 从数据集中随机选择 k 个点作为簇心。（实际上初始化时候选择的点会影响最终的结果，有很多初始化的算法）。
2. 计算每个点到簇心的距离，将每个点划分到距离最近的簇心所在的簇。
3. 计算每个簇的新簇心（质心），即簇内所有点的平均值。
4. 重复 2、3 步骤，直到簇心不再变化，（又或者连续多次变化值很小，可以定义一个阈值）。

KNN 检索

KNN 检索的思路很简单，就是计算待检索向量与数据集中每个向量的距离，然后排序，取前 N 个最近的向量。这里的距离可以是欧式距离，也可以是余弦距离等。KNN 其实就是暴力计算，计算量大，不适合大规模数据的检索。

暴力计算对上述的例子来说很简单，我们只需要把用户检索的 Query 的特征向量和库里所有特征逐个计算距离然后排序取前 N 个结果即可。

$ d([100, 200, 100, 100], [300, 200, 100, 400]) = \sqrt{(100 - 300)^{2} + (200 - 200)^{2} + (100 - 100)^{2} + (100 - 400)^{2}} = 360.6 $ $ d([200, 300, 200, 500], [300, 200, 100, 400]) = \sqrt{(200 - 300)^{2} + (300 - 200)^{2} + (200 - 100)^{2} + (500 - 400)^{2}} = 200.0 $ $ d([300, 400, 300, 400], [300, 200, 100, 400]) = \sqrt{(300 - 300)^{2} + (400 - 200)^{2} + (300 - 100)^{2} + (400 - 400)^{2}} = 282.8 $ $ d([400, 500, 500, 600], [300, 200, 100, 400]) = \sqrt{(400 - 300)^{2} + (500 - 200)^{2} + (500 - 100)^{2} + (600 - 400)^{2}} = 547.7 $ $ d([500, 600, 600, 200], [300, 200, 100, 400]) = \sqrt{(500 - 300)^{2} + (600 - 200)^{2} + (600 - 100)^{2} + (200 - 400)^{2}} = 700.0 $

由此可得，与 [300, 200, 100, 400] 最相似的是 [200, 300, 200, 500]，其次是 [300, 400, 300, 400]，以此类推。

一般来说可以使用像 K-D 树等的方法构建高维空间的检索结构减少计算量，但是对于维度较高的向量效果有限，还是不适合做大规模的检索。

ANN 检索

倒排

倒排索引在传统文本检索领域很常见，比如我们有一个文档集合，每个文档都有一个 ID，我们需要根据某个关键词找到对应的文档，除了暴力遍历文档集合，我们还可以 构建一个倒排索引，这个索引是文档中所有分词对应的文档 ID 集合，这样我们就可以快速找到对应的文档了。举例，现在我们有一些文档如下：

doc_1: "我爱北京天安门"
doc_2: "我爱北京故宫"
doc_3: "我爱北京天坛"

这时对这些文档做倒排索引，我们可以得到如下的索引：

我: [doc_1, doc_2, doc_3]
爱: [doc_1, doc_2, doc_3]
北京: [doc_1, doc_2, doc_3]
天安门: [doc_1]
故宫: [doc_2]
天坛: [doc_3]

如果用户输入 "天安门" 这个关键词，则可以找到 doc_2 这个文档，而不需要暴力检索所有文档了。

倒排本质是缩小检索范围。在向量检索中，我们也可以通过类似的方法来缩小检索范围。但是难点在于，向量是连续的，而文本是离散的，文本数据是有穷的，而向量数据 是无穷的，不能像文本检索那样直接用一个哈希表来存储。这时候我们可以使用聚类中心的方法来实现倒排。聚类中心的本质是把向量空间划分成若干个区域，相当于把 连续的数据离散化，这些在数字信号处理很常用。

首先解释一下什么是聚类中心，比如拿前面的数据，我们为了方便只拿前 2 个维度的数据作为例子，我们可以把这些数据画在二维坐标系中，如下图所示：

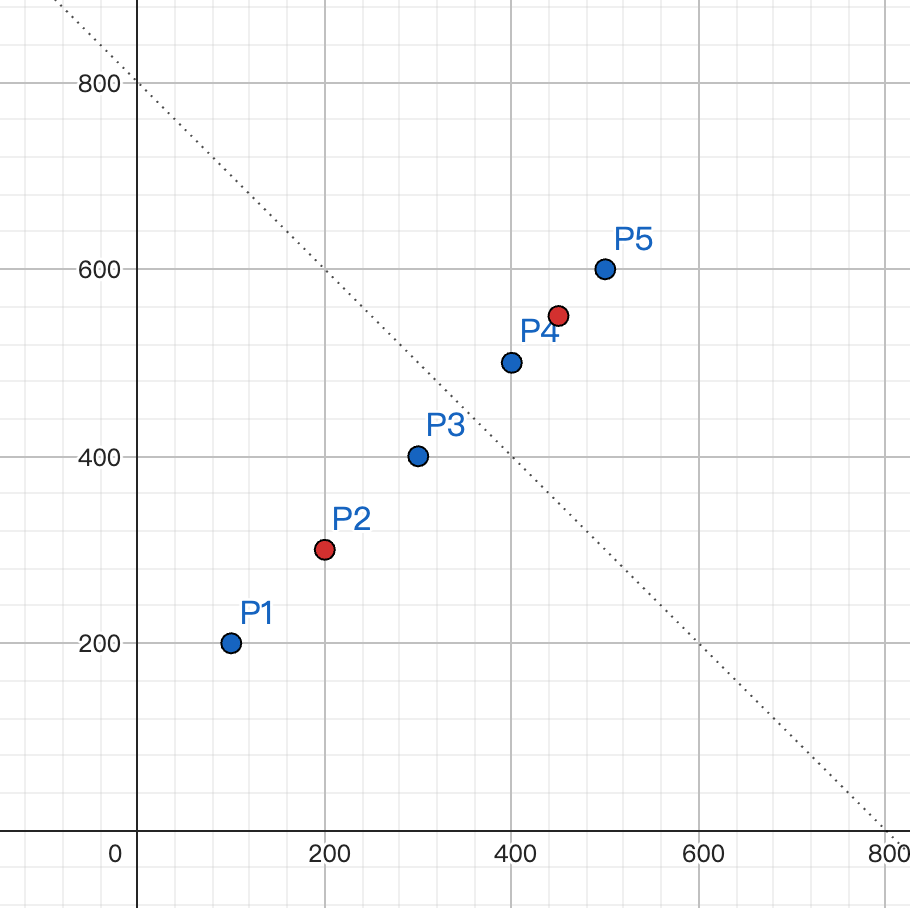
如上图， 我们把这 5 个向量分成 2 组数据（多少组是可以指定的，根据数据量和期望的准确率来决定），每组数据有一个聚类中心，即 $ P_{1} $、$ P_{2} $、 $ P_{3} $ 的聚类中心是 $ P_{2} $，$ P_{4} $、$ P_{5} $ 的聚类中心是 $ P_{5} $，这个聚类中心即是这组数据的代表，聚类中心到这组数据的其他点 的距离是最短的。

关于聚类的方法，常用的是 K-means 算法，即通过多轮迭代无限找到接近最优解的聚类中心， 这里不做展开。

通过聚类我们就把连续的数据离散化了，这样就可以用哈希表来存储了，比如我们可以用 $ P_{2} $ 的哈希表存储 $ P_{1} $、$ P_{2} $、 $ P_{3} $ 了。 此时我们检索只需要把用户输入的 Query 和聚类中心进行比较即可。这里还有一个问题，假设我期望 返回 TOP3 的结果，用户输入的 Query 特征向量是 (300, 400)，期望的结果应该是 $ P_{2} $、$ P_{3} $、$ P_{4} $，但是由于我们锁定了 1 个聚类中心，导致结果是 $ P_{1} $、$ P_{2} $、 $ P_{3} $。通常地，我们会多搜索几个聚类中心里面的结果再排序来得到更优解。

cluster_1(200, 300): [(100, 200), (200, 300), (300, 400)]
cluster_2(450, 550): [(400, 500), (500, 600)]

HNSW

HNSW 是一种基于图的 ANN 检索算法，其全称是 Hierarchical Navigable Small World。HNSW 的思想是 通过构建一个图来实现 ANN 检索，这个图是一个稠密图，每个节点都有很多边，这样就可以快速找到相似的节点了。

了解 HNSW 前要先了解 NSW。NSW 的想法是通过构建一个无向图来表示向量之间的相似图，我们使用上面的向量后面 2 维做例子：

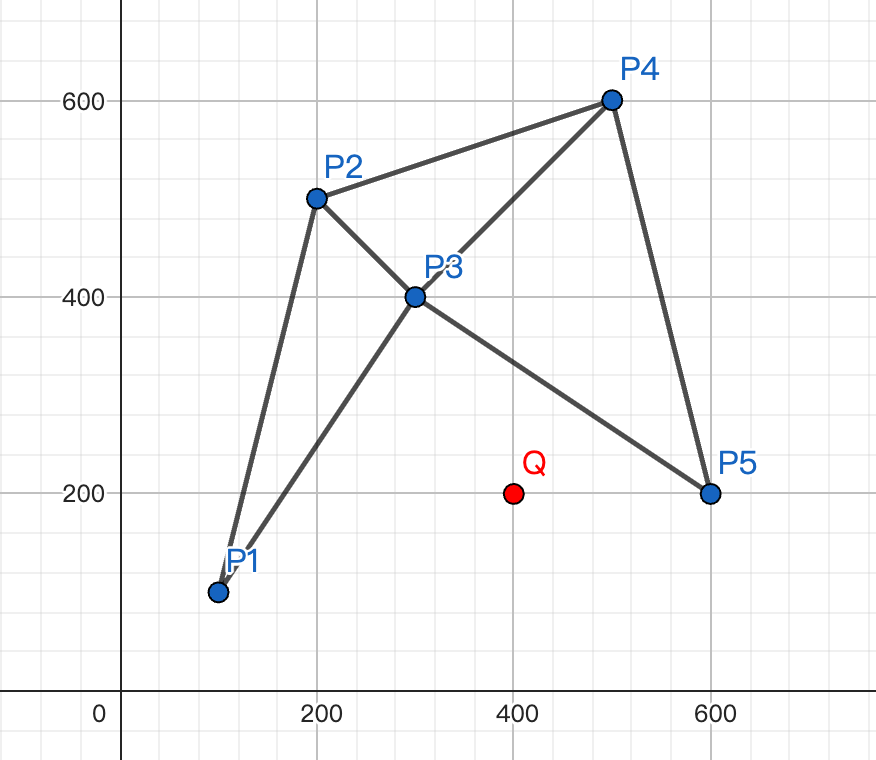
这个图的实际上是 m=2，即构建时每个点都会连接离自己最近的 2 个点，这样就构建了一个无向图，因此所有点的度至少都是 2。假设我们现在有一个点 Q(400, 200)，需要找到离它最近的点。我们先随机找到一个点 $ P_{1} $，然后找到 $ P_{1} $ 的邻居点 $ P_{2} $ 和 $ P_{3} $，显然 $ P_{3} $ 离 Q 点更近。然后找到 $ P_{3} $ 的邻居点 $ P_{1} $、$ P_{2} $、$ P_{4} $ 和 $ P_{5} $，显然 $ P_{5} $ 离 Q 点更近。染好找到 $ P_{5} $ 的邻居点 $ P_{3} $ 和 $ P_{4} $，发现距离变大了，遍历结束。这样我们就找到了离 Q 点最近的点 $ P_{5} $。

看完 NSW 后我们看一下 HNSW。HNSW 有点类似跳表（skip list），我们拿出论文里的例子图：

HNSW 的思想是每层随机选出一些点来组成这一层的图，从下往上看即每层都会比前一层少一些点。构建的时候这个点属于哪一层使用随机函数来决定，这个随机函数是

$ f(x) = min(\lfloor -ln(unif(0..1)) * m_{L} \rfloor, L) $。$ unif(0..1) $ 是 0 到 1 之间均匀分布的随机函数，$ -ln(x) $ 的函数图像如下：

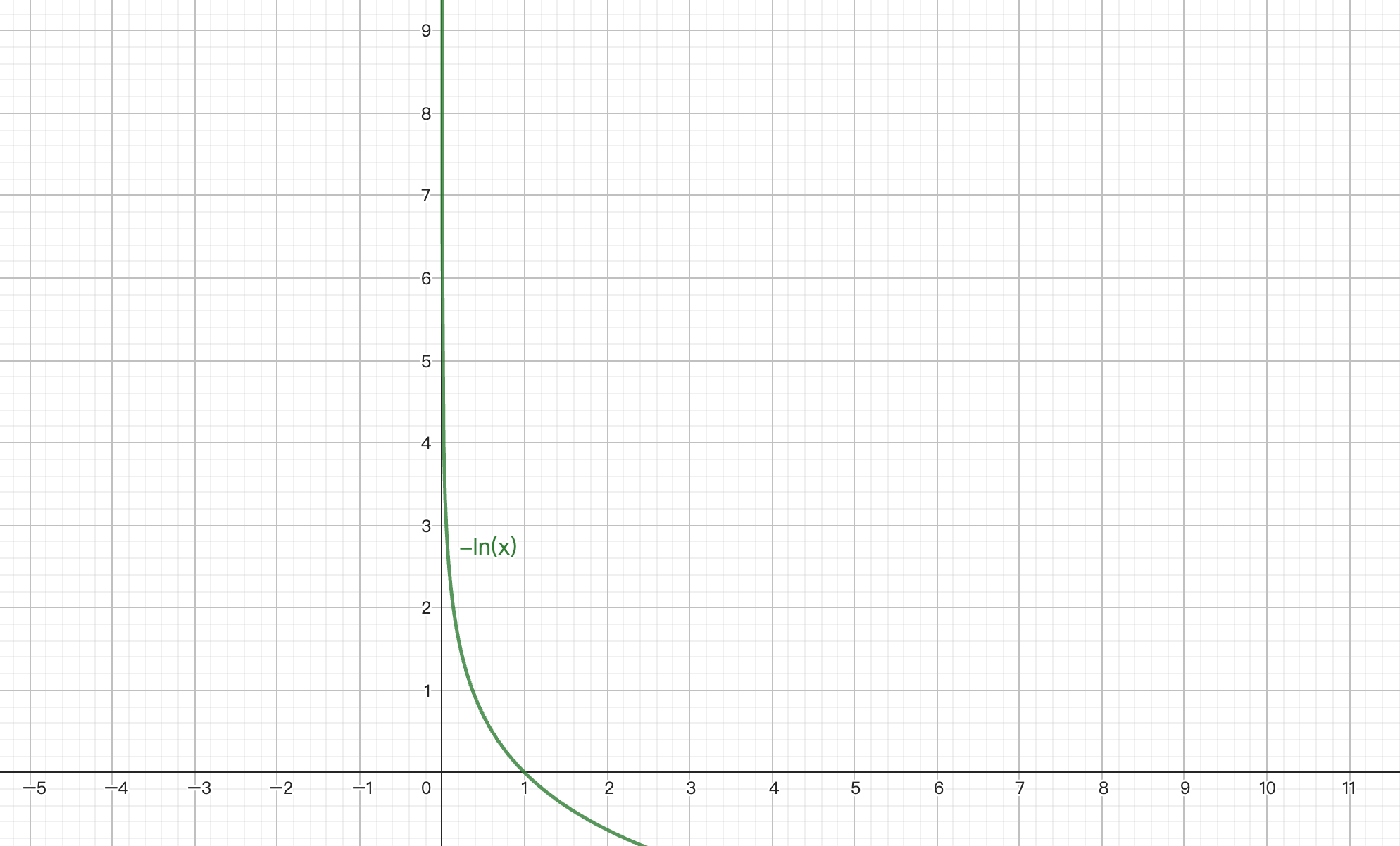
而 $ m_{L} $ 和 $ L $ 是用户输入的常数值。因此，一个点属于哪一层是随机的，而且往往是更大概率属于更下面的层。每个点可能属于 [0, L] 层，如果一个点 在第 l 层，那么它也一定在 0, 1, 2... l-1 层。

检索时从上往下遍历，因为有了更少的点所以可以更快逼近到期望值。

PQ 量化

PQ(Product Quantization) 量化 是一种将高维向量量化为低维向量的方法，其思想是 将一个高维向量切分为多个子向量，然后对每个子向量进行聚类，并通过使用码本的方法减少向量存储在内存中的大小。可以说 PQ 量化的模板是减少计算量和内存消耗。 还是使用之前的例子，我们把 4 维向量切分成 2 组 2 维向量，每组进行聚类，聚类分组每组 4 个。即：

# 纵向切分向量，降低维度
[100, 200, 100, 100] -> [100, 200], [100, 100]
[200, 300, 200, 500] -> [200, 300], [200, 500]
[300, 400, 300, 400] -> [300, 400], [300, 400]
[400, 500, 500, 600] -> [400, 500], [500, 600]
[500, 600, 600, 200] -> [500, 600], [600, 200]

# 每组分别进行聚类，聚类中心 4 个
# 组1， cluster 0，聚类中心是 (100, 200)
[100, 200]
# 组1，cluster 1，聚类中心是 (200, 300)
[200, 300]
# 组1，cluster 2，聚类中心是 (300, 400)
[300, 400]
# 组1，cluster 3，聚类中心是 (450, 550)
[400, 500]
[500, 600]
# 组2，cluster 0，聚类中心是 (100, 100)
[100, 100]
# 组2，cluster 1，聚类中心是 (250, 450)
[200, 500]
[300, 400]
# 组2，cluster 3，聚类中心是 (500, 600)
[500, 600]
# 组2，cluster 4，聚类中心是 (600, 200)
[600, 200]

分组后，我们为每组分别建立一个码本，码本的大小是 2，即每个码本有 4 个码字，每个码字可以压缩成 2bit。 对应上面的例子，我们可以把 cluster 编码使用 0、1、2 和 3 来编码，每个向量可以压缩成 4bit 大小，即 m=2，k=4。

[100, 200, 100, 100] -> [100, 200], [100, 100] -> [0, 0]
[200, 300, 200, 500] -> [200, 300], [200, 500] -> [1, 1]
[300, 400, 300, 400] -> [300, 400], [300, 400] -> [2, 1]
[400, 500, 500, 600] -> [400, 500], [500, 600] -> [3, 2]
[500, 600, 600, 200] -> [500, 600], [600, 200] -> [3, 3]

另外我们保存每个码本对应的聚类中心：

组1：
0 -> (100, 200)
1 -> (200, 300)
2 -> (300, 400)
3 -> (450, 550)
组2：
0 -> (100, 100)
1 -> (250, 450)
2 -> (500, 600)
3 -> (600, 200)

上面的例子我们可以发现，会有可能用同几个码字来表示不同的向量，所以会存在误差，这个误差就是量化误差。量化误差的大小和码本的大小有关，码本越大，误差越小。 论文原文中有提到，如果 k=256，m=8，那么量化误差可以控制在 1% 以内。

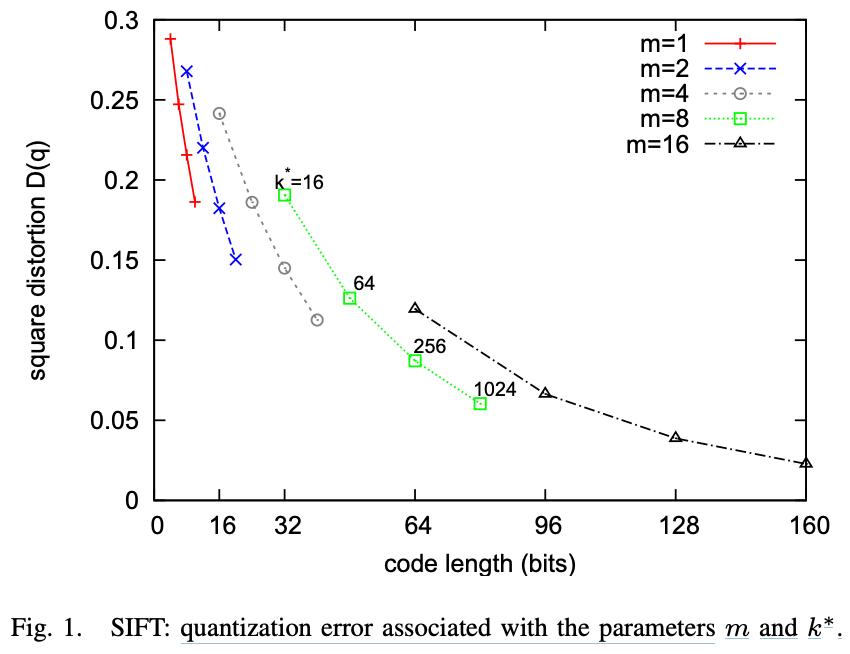
上面几种方法不一定要单独使用，可以组合使用。比如我们可以使用 HNSW + 倒排组合，先通过倒排找到一些候选集合，然后通过 HNSW 比较准确地找到候选点，这个 其实是华为云检索服务的做法。也可以通过二级聚类空间的方法，就是通过两次倒排检索找到结果，这个其实是百度 GNOIMI 的做法。

应用

FAISS

我们在了解上述的各种算法后，可以使用已有的轮子进行建库，只需要调参即可。使用时分成两步：建库、检索。建库是把所有向量数据都存储到索引中，并写 入文件方便部署，可以称为近线或离线部分。检索是在线部分，读取离线建库好的索引并加载到内存中，然后对外提供检索服务。

建库时我们需要指定一种索引，可以使用 Index Factory 通过字符串就可以选择索引了，参考这个文档。 这里列举一些使用的索引：

索引	说明
Flat	只进行向量摊平存储，也就是暴力搜索
HNSW8,Flat	HNSWx，这个 x 表示 NSW 图中每个点的边的数量。这个边越多检索越快，效果也会更好，但是占用的内存也会越多，建库时间也会更长
IVF128,Flat	IVFx，这个 x 表示倒排索引中聚类中心的个数
IVF128,PQ16	表示使用 PQ 量化存储索引。PQx，这个 x 表示把向量分成 x 组，即上文 m 的值
IVF128,PQ16x12	PQaxb，这个 a 表示把向量分成 a 组，每组使用 12 个 bit 来存储，默认是 8bit。12bit 即 4096 个码字，8bit 是 256 个码字，12bit 的索引会更大，但是误差会更小，检索效果会更好

算法对比

我们使用 Google Landmarks Dataset v2 数据集来测试不同算法的性能。我仅使用了前 20 个 tar 共 173586 个图片，使用 ResNet50 提取特征。这里因为使用的数据集较少就不做 PCA 降维了，直接 使用 2048 维特征。测试的机器是 MacBook M1 Pro。

训练脚本：

import faiss
import numpy as np
import time

IDX_PATH = 'indexes'

IDX_LIST = [
    {
        'name': 'brute_force_search',
        'idx_str': 'Flat',
    },
    {
        'name': 'hnsw8',
        'idx_str': 'HNSW8,Flat',
    },
    {
        'name': 'hnsw64',
        'idx_str': 'HNSW64,Flat',
    },
    {
        'name': 'ivf128',
        'idx_str': 'IVF128,Flat'
    },
    {
        'name': 'ivf1024',
        'idx_str': 'IVF1024,Flat',
    },
    {
        'name': 'hnsw8_pq16',
        'idx_str': 'HNSW8_PQ16',
    },
    {
        'name': 'hnsw8_pq64',
        'idx_str': 'HNSW8_PQ64',
    },
    {
        'name': 'ivf128_pq16',
        'idx_str': 'IVF128,PQ16',
    },
    {
        'name': 'ivf128_pq64',
        'idx_str': 'IVF128,PQ64',
    },
]


def load_data():
    labels = []
    feats = []
    with open('feat_resnet50.csv', 'r') as fp:
        for line in fp:
            line = line.strip()
            data = line.split('\t')
            if len(data) != 2:
                continue
            label, feat_txt = data
            feat = np.fromstring(feat_txt, dtype=np.float32, sep=',')
            labels.append(label)
            feats.append(feat)
    return np.array(labels), np.array(feats)


def train():
    _, feats = load_data()

    for item in IDX_LIST:
        print('start build %s index' % item['name'])
        start_time = time.time()
        idx = faiss.index_factory(feats[0].shape[0], item['idx_str'], faiss.METRIC_L2)
        idx.train(feats)
        idx.add(feats)
        end_time = time.time()
        faiss.write_index(idx, '%s/%s.idx' % (IDX_PATH, item['name']))
        print('finish build %s index, cost %.2f' % (item['name'], end_time-start_time))

def search():
    labels, _ = load_data()
    test_feats = load_test_feats()

    idx = faiss.read_index('%s/%s.idx' % (IDX_PATH, 'ivf128_pq64'))
    d, i = idx.search(test_feats, 1)
    print(d) # d 为检索向量与检索结果的距离
    print(i) # i 为检索结果的下标索引，可以使用 labels[i] 找到对应的标签
        
if __name__ == '__main__':
    train()
    search()

测试结果：

算法	建库时间	索引大小	检索内存使用	检索时间	召回率	准确率
Flat	0.28s	1356.14M	1709.47M	16.69s
HNSW8,Flat	9.88s	1369.49M	1670.22M	1.22s
HNSW64,Flat	1271.76s	1443.55M	1725.30M	10.22s
IVF128,Flat	0.77s	1358.47M	1665.59M	8.66s
IVF1024,Flat	6.38s	1365.47M	1810.64M	1.9s
HNSW8_PQ16	15.95s	17.99M	379.48M	0.38s
HNSW8_PQ64	85.91s	25.94M	441.94M	0.48s
IVF128,PQ16	15.47s	6.97M	400.33M	0.44s
IVF128,PQ64	54.31s	14.92M	416.73M	0.71s